Getting-real-world-coordinates-from-image-frame

Why do we need it?

Our goal was to convert coordinates on the image to real world coordinates e.g. we wanted to know object's position relative to robot's position. This is necessary to make a robot understand, where the objects are relative to his position. More generally speaking, this is also needed to figure out the absolute coordinates on the football field.

Pinhole camera model

We used the pinhole camera model. I am not going to describe all the theory for that, here is the main formula that describes how the objects are projected onto the screen.

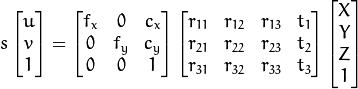
To learn about this model, there are good enough resources available (start with wiki and udacity), but focus more on the overall idea, problems we had and tools we used.

How to map coordinates from 3D to 2D?

To be able to convert between two coordinate systems, we need to know the intrinsic parameters and extrinsic parameters of the camera. The former describes how any real world object is projected to camera’s light sensors. It consists of parameters such as camera’s focal length, principal point and skew of the image axis. The latter gives information about camera’s pose in the observed environment (3 rotations and 3 translations as we live in a 3-dimensional world). To convert a 2-dimensional screenpoint into a 3-dimensional world point, we also need to make an extra assumption that all the objects that interest us are on a specific plane (e.g. on the floor where Z=0).

How did we find out the camera parameters and the pose?

We based our calibration system on the OpenCV implementation of an algorithm that gathers tries to match screen coordinates with known real-world coordinates and hence tries to estimate the required parameters by using many different observations . Because we only need to find those parameters once, we did not see a need for developing anything more complex for that. We found useful OpenCV functions specially designed for finding the camera matrix (intrinsic parameters) and rotation-translation matrix (extrinsic parameters) (see documentation for calibrateCamera(), findChessboardCorners(), drawChessboardCorners() and projectPoints() also tutorial might be useful). If you are interested in the inner workings of these algorithms, you can go and read the documentation or the source code. After collecting all results in terms of these parameters, we were able to convert real world 3D-points onto the image plane. But as this wasn’t our goal (we wanted 2D -> 3D) we had to reverse this equation.

How to map 2D point to 3D?

There was a bit of chaos and many “wasted” days in terms of reversing this operation. We had problems with inverting matrices. We took the model Opencv Mat::inv() didn’t give right results and some matrix pseudo inverse seemed to be not working – probably these matrices weren’t invertible.

TODO: Dig deeper, what was the problem with not being able to invert those matrices. TODO: A picture of previous formula altered.

In the end we solved equations with Cramer’s rule.

Changing plane rotation while robot is on the move

We noticed quite aggressive tilting happening one the image while Nao was moving, in figures it was approximately +5...-5 degrees over orthogonal axis relative to the image frame (TODO: something more convincing needed as a figure). Visually it seemed a lot - have a look.

Angle what Nao's torso is moving can be easily measured with AL::ALValue ALMemoryProxy::getData("device"). Next we made an assumption that Nao's torso is rotating the same amount as it's head and made connection fixed between torso and head. Having obtained the angle we had to make camera pose dependent on the robot rotation. After some thinking and drawing we found that we had to update camera rotation matrix according to Nao's torso rotation.

Performance

TODO: