EchemDID

Testing with variable cut-offs:

/home/kristian/sshfs/rocket/echemtest/validation/forces_capa/test_cutoff

The default cut-off for the Coulombic interaction for the Qeq scheme used in EchemDID is 15 Å. Did tests with 20, 30,40.... 100 Å with the distance between plates being 18 Å. Found out that at higher cut-off values, the scheme breaks down entirely. The force and charge distributions become increasingly unphysical. Probably better to use the pre-determined cut-off value parametrized for the force field, even though this might cause the known problems.

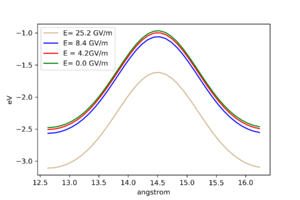
Potential landscapes for different electric fields

Did tests with different electric fields by moving a test atom on 100 surface by one lattice constant. We can see, that greater the electric field, lower the potential energy of an adatom.

16.10

Ran the minimization of an adatom on the tiltsurface. It worked, but does not give anything that interesting. The forces go to 0 if the tolerance is low enough, as should be. At least it does not crash, meaning it is possbile to simulate such a system. Found out that single atom temperature has no meaning - which should be well understood. Also thats the reason it is not possible or worthwhile to run dynamics with only the adatom unfrozen. Tried to run the whole tiltplane system at 300 K, which gave bogus results. Furthermore, more sensitive tests should be run only on minimized systems. Read https://doi.org/10.1016/j.ijsolstr.2007.09.010. It seems, that the electric field gradient is the driving force, although they look from contiinum-analytical perspective. Also it seems from their arguments, that the electric field gradient runs the diffusion anyways, without the necessary parallel components(dipoles)

Found several other methods which include the effect of the electric field. For example: https://doi.org/10.1063/1.5029877 Says, that they got rid of the cut-off problem. Hard to understand how from the paper, seems just a bit modified $\chi_{effective} -V/2$. They also have a fully filled system(no vacuum)

Also, the Van Duin paper for Ni/H2O interface supports the $\chi_i\rightarrow \chi_i + \mathbf{r_i}\cdot \mathbf{E}$ formulation. Although they have a tiny slab and fully filled, so the cut-off problem might now arise as heavily

The main question: in the case of p-plate cap, is the effect of the electric field to change: $$\chi_i \rightarrow \chi_i \pm \frac{V}{2}$$

Or $$\chi_i \rightarrow \chi_i \pm \mathbf{r_i} \cdot \mathbf{E}$$

Where $V$ is the external potential difference, Both cannot be right at the same time. Or do they correspond to different physical models? If so, to which models