EchemDID: Difference between revisions
No edit summary |
No edit summary |
||
| Line 21: | Line 21: | ||
Read https://doi.org/10.1016/j.ijsolstr.2007.09.010. It seems, that the electric field gradient is the driving force, although they look from contiinum-analytical perspective. Also it seems from their arguments, that the electric field gradient runs the diffusion anyways, without the necessary parallel components(dipoles) | Read https://doi.org/10.1016/j.ijsolstr.2007.09.010. It seems, that the electric field gradient is the driving force, although they look from contiinum-analytical perspective. Also it seems from their arguments, that the electric field gradient runs the diffusion anyways, without the necessary parallel components(dipoles) | ||
Found several other methods which include the effect of the electric field. '''The main question: in the case of p-plate cap, is the effect of the electric field to change $$\xsi$$''' | |||
[[File:Selection 003.png|thumb]] | [[File:Selection 003.png|thumb]] | ||
Revision as of 15:06, 16 October 2018
Testing with variable cut-offs:
/home/kristian/sshfs/rocket/echemtest/validation/forces_capa/test_cutoff
The default cut-off for the Coulombic interaction for the Qeq scheme used in EchemDID is 15 Å. Did tests with 20, 30,40.... 100 Å with the distance between plates being 18 Å. Found out that at higher cut-off values, the scheme breaks down entirely. The force and charge distributions become increasingly unphysical. Probably better to use the pre-determined cut-off value parametrized for the force field, even though this might cause the known problems.
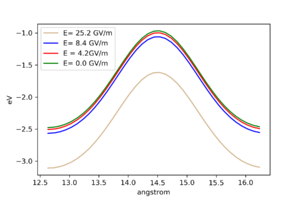
Potential landscapes for different electric fields
Did tests with different electric fields by moving a test atom on 100 surface by one lattice constant. We can see, that greater the electric field, lower the potential energy of an adatom.
16.10
Ran the minimization of an adatom on the tiltsurface. It worked, but does not give anything that interesting. The forces go to 0 if the tolerance is low enough, as should be. At least it does not crash, meaning it is possbile to simulate such a system. Found out that single atom temperature has no meaning - which should be well understood. Also thats the reason it is not possible or worthwhile to run dynamics with only the adatom unfrozen. Tried to run the whole tiltplane system at 300 K, which gave bogus results. Furthermore, more sensitive tests should be run only on minimized systems. Read https://doi.org/10.1016/j.ijsolstr.2007.09.010. It seems, that the electric field gradient is the driving force, although they look from contiinum-analytical perspective. Also it seems from their arguments, that the electric field gradient runs the diffusion anyways, without the necessary parallel components(dipoles)
Found several other methods which include the effect of the electric field. The main question: in the case of p-plate cap, is the effect of the electric field to change $$\xsi$$