Getting-real-world-coordinates-from-image-frame

Why do we need this part?

Our purpose was to convert items on the image to real world coordinates e.g. we wanted to know item placement relative to robot's placement. This is necessary to make robot understand where are objects relative to him, and if we are watching a bigger picture, this is necessary to make robot know where it is relative to the soccer field.

Pinhole camera model

For this, we used pinhole camera model. I am not going to describe all the theory for that, here is what pinhole model does in one formula:

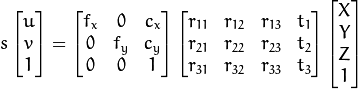
To learn about this model there are good enough resources available (start with wiki and udacity), but more focus on overall idea, troubles we had and tools we used.

How to map coordinates from 3D to 2D?

To be able to transform between two coordinate systems it is needed to know camera intrinsic parameters and extrinsic parameters. Former describes how any real world object arrives to camera’s light sensor. It consists of parameters such as camera’s focal length, principal point and skew of the image axis. Latter gives information about camera’s pose in the observed environment (3 rotations and 3 translations as we live in a 3 dimensional world). To convert 2 dimensional point into 3 dimensional world we also need to make an extra assumption that objects that interest us are on a plane that we determine.

How did we get camera parameters and pose? We based our calibration system on opencv implementations of finding all of these parameters. Didn’t see any need to make anything topnotch in terms of speed, because we will need to get all these parameters only once and we can use them .. forever. We found useful opencv functions specially designed for finding camera matrix (intrinsic parameters) and rotation-translation matrix (extrinsic parameters) (see documentation for calibrateCamera(), findChessboardCorners(), drawChessboardCorners() and projectPoints() also tutorial might be useful). If you are interested in algorithms what makes it work, go watch the documentation or source code. After collecting all winnings in terms of these parameters we were able to convert real world 3D points onto image plane. But as this wasn’t our goal (we wanted 2D -> 3D) we had to keep going.

How to map 2D point to 3D?

There was a bit of chaos and many “wasted” days in terms of reversing this operation. We had problems with inverting matrices. We took the model Opencv Mat::inv() didn’t give right results and some matrix pseudo inverse seemed to be not working – probably these matrices weren’t invertible.

TODO: Dig deeper, what was the problem with not being able to invert those matrices. TODO: A picture of previous formula altered.

In the end we solved equations with Cramer’s rule.

Changing plane rotation while robot is on the move

We noticed quite aggressive tilting happening one the image while Nao was moving, in figures it was approximately +5...-5 degrees over orthogonal axis relative to the image frame (TODO: something more convincing needed as a figure). Visually it seemed a lot - have a look.

Angle what Nao's torso is moving can be easily measured with AL::ALValue ALMemoryProxy::getData("device"). Next we made an assumption that Nao's torso is rotating the same amount as it's head and made connection fixed between torso and head. Having obtained the angle we had to make camera pose dependent on the robot rotation. After some thinking and drawing we found that we had to update camera rotation matrix according to Nao's torso rotation.

Performance

TODO: